我国传统数学著作《数书九章》中的秦九韶算法与西方的海伦公式有异曲同工之妙,那如何用秦九韶算法来推导海伦公式呢?
一、秦九韶算法
1247年,数学家秦九韶提出了一种多项式简化算法,被称为秦九韶算法。秦九韶算法记录在《数书九章》中,他对高次方程的数值解法与一次同余问题的解法进行了系统总结和发展,提出了相当完备的“正负开方术”和“大衍求一术”。这也让秦九韶成为我国古代数学家的杰出代表,他的研究为中国古代数学发展带来了广泛而深远的影响。
秦九韶算法能够将一元n次多项式的求值问题转化为n个一次式。通过使用这种算法对计算过程的简化有很大作用,即便是在现代,利用计算机解决多项式的求值问题,秦九韶算法也是比较清晰简便的方式。对于一元n次多项式的求值,通常需要经过(n+1)*n/2次乘法,秦九韶算法的先进点就在于它只需要进行n次乘法,从而大大缩短人工简化的运算过程。
二、海伦公式
已知一个三角形的三边长,怎么计算三角形的面积?这是我们在几何中经常碰到的问题。古希腊著名数学家海伦写了一本《测量仪论》,上面记载着一个重要公式:
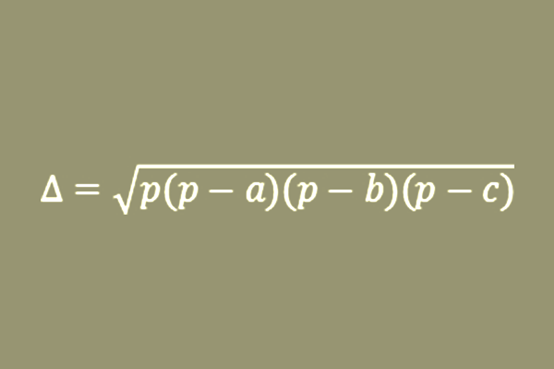
这里,“△”指三角形的面积,a、b、c是三角形各边长。海伦对这个公式做出了证明,所以后人称这个公式为海伦公式。
根据海伦公式,假设平面内的一个边长分别为a、b、c的三角形,三角形的面积S和其中p为周长的一半可求,即:
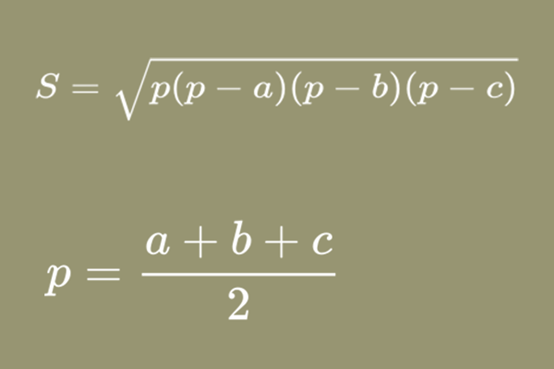
三、如何用秦九韶算法推导海伦公式
秦九韶算法和海伦公式本质上的原理十分相似,因此用秦九韶算法来推导海伦公式对于数学学习者来说其实并不难。证明过程如下:
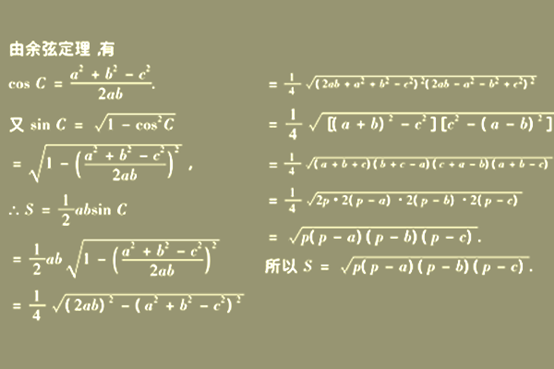
要想学好数学,关键在于平时的积累,把平时的积累理解透彻转化成自己所学,有助于我们在面对新问题的时候找出更多合理的解决办法。
本文由山东省莱州市文峰中学二级教师李奕樊进行科学性把关。

科普中国中央厨房
新华网科普事业部
科普中国-科学原理一点通
联合出品
更多精彩内容,请下载科普中国客户端。
本作品为“科普中国-科学原理一点通”原创,转载时务请注明出处。